- Innovaciones
- Artículos sobre la aplicación de PCI
- Trading de Portfolios
Optimización del Portfolio a través del Método PQM (Parte 2)
Supongamos que un inversionista está realmente dispuesto a aceptar un nivel de riesgo mas alto para aumentar el rendimiento esperado del portfolio. Deje que la desviación típica máxima aceptable de la rentabilidad de la cartera sea 2,5%. Vamos a llevar a cabo el procedimiento de optimización de los coeficientes de peso para la búsqueda de la máxima rentabilidad de la cartera con una restricción adicional de la desviación estándar (no debe superar el 2,5%).
La solución nos lleva a la siguiente composición de P3: Los Stocks MCD obtuvieron nuevamente el mayor peso (61,3%). Entonces el DIS (21,74%), HON (14,17%), IBM (1,61%) y HD (0,84%) varió en el orden descendiente. Los stocks KO consiguieron peso creo, y no se incluyen en el portfolio P3.
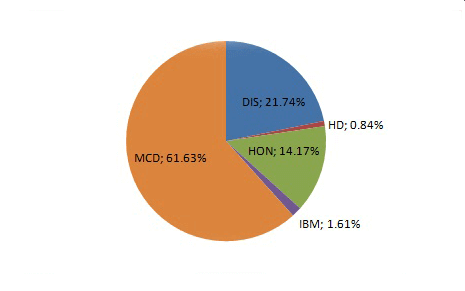
Como resultado de ello, el portfolio P3, formado para maximizar el rendimiento esperado bajo la condición de que no exceda el nivel de desviación estándar de 2,55- dio el retorno mensual esperado de 0,65% y el ratio de Sharpe de 0,26.
Tabla 4: Retornos concretados, desviaciones estándar y ratios de Sharpe de los portafolios P1, P2 y P3
| P1 | Р2 | Р3 | |
| Mean Return | 0.49% | 0.24% | 0.40% |
| StDev | 4.25% | 5.73% | 4.51% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 |
A través de las herramientas PCI, vamos a construir un grafico que refleje la dinámica del portfolio P3, incluyendo cinco acciones con sus pesos correspondientes en la parte base, y el indice de promedio insdustrial de Dow Jones en la parte cotizada.
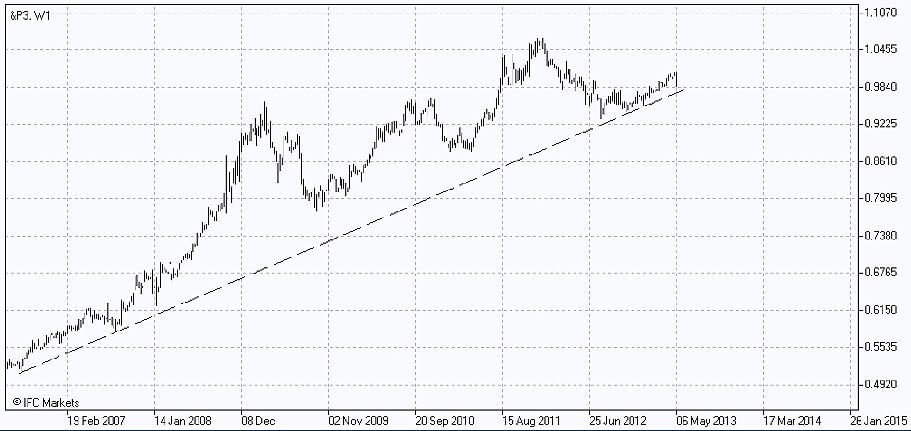
Podemos seguir como antes una estructura cada vez mayor. El crecimiento durante todo el periodo observado llegó a ser más considerable que en el caso de P2, pero la fluctuación durante la crisis parece más importante. Un resultado directo del aumento del riesgo permisible.
Para hacer el cuadro bien completo, vamos también a construir un portfolio para un inversor que busca deshacerse del máximo riesgo, mediante la diversificación. Para ello, vamos a recurrir al procedimiento de optimización de los pesos de las acciones disponibles, y la búsqueda del valor mínimo de la desviación estándar. El portfolio P4 se caracteriza por el siguiente conjunto de pesos:
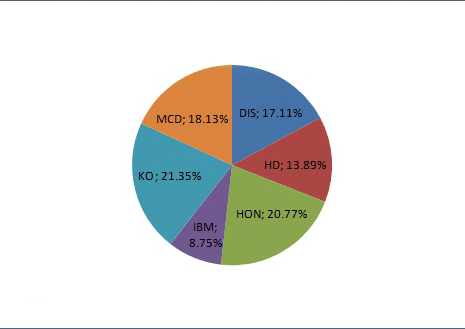
El diagrama muestra que esta vez, el coeficiente de mayor peso, cayó sobre el Stock KO (21,35%), después de todo era la acción para que nos dieran la menor desviación estándar de datos de entrada. Entonces el HON (20,77%), MCD (18,13%), DIS (17, 11%), HD (13, 89%) e IBM (8,75%), que varió en un orden de peso decreciente. Este portfolio se caracteriza por la rentabilidad esperada del 0,45%, una desviación estándar de 1,60% y el ratio de Sharpe de 0,28.
| P1 | Р2 | Р3 | Р3 | |
| Mean Return | 0.46% | 0.52% | 0.65% | 0.45% |
| StDev | 1.74% | 1.72% | 2.50% | 1.60% |
| Sharpe Ratio | 0.26 | 0.30 | 0.26 | 0.28 |
Las herramientas PCI nos volverán a ayudar en la construcción de la tabla del portfolio, y estimando su comportamiento con el índice Down Jones Industrial promedio, en un periodo de tiempo examinado.
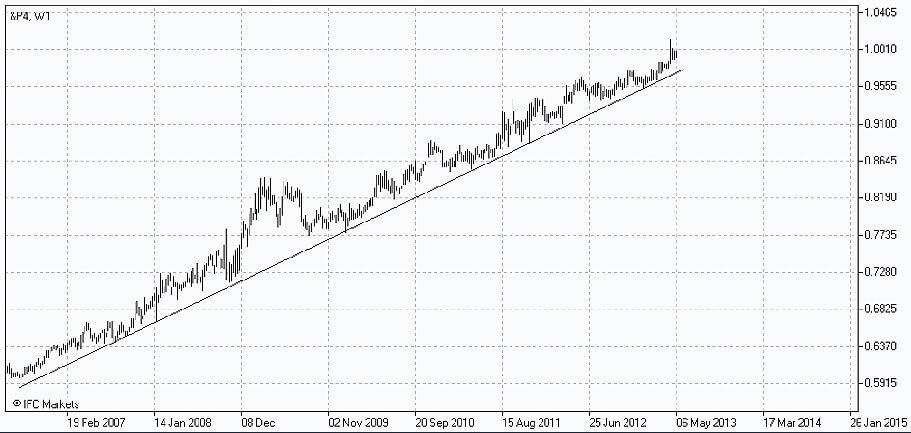
Es increíble lo tranquilo que parece el comportamiento del portfolio P4. Aunque el crecimiento absoluto durante todo el periodo es menor que en el caso de los portfolios formados previamente, comparativamente con rango de estrecho margen de fluctuación, lo que refleja una menor volatilidad, que tiene sus ventajas.
Si graficamos los cuatro portfolios (P1, P2, P3, P4), en las coordenadas de riesgos y rendimiento, solamente podemos confirmar que el portfolio P2 (relación máxima Sharpe) se prefiere el "azar" a que el porfolio P1, ya que su posición (en el sector izquierdo superior con respecto a P1), indica una mayor rentabilidad y una menor desviación estándar.
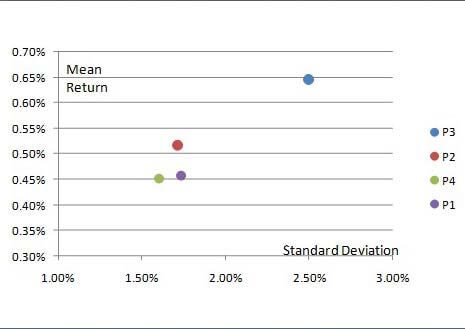
La elección entre los portfolios P2, P3 y P4, dependerá de las preferencias y restricciones individuales del inversionista. Si un inversionista está dispuesto a aceptar el nivel de riesgo relativamente alto de su elección, probablemente cambie al portfolio P3, con el mayor retorno esperado (entre las opciones consideradas). Si un inversionista busca minimizar los riesgos, su elección puede ser la cartera P4, que tiene la desviación estándar mas baja (entre las opciones consideradas). Lo llamaríamos portfolio P2, un portfolio equilibrado, con el mejor rendimiento por unidad de riesgo.
Los gráficos construidos a través del método PQM y la herramienta PCI, comprueban visualmente las oportunidades de aplicar los principios contemporáneos de la teoría del Portfolio. En base a las estimaciones cuantitativas de riesgo, el retorno y la covarianza de varias acciones que hemos encontrado una variedad de Portfolios "exitosos" los cuales han ido sistemáticamente superando el mercado en los últimos años, y al mismo tiempo se han reunido numerosas preferencias de inversión. Nuestro análisis se basa en solo siete activos (6 acciones + índex) de la misma clase de instrumentos financieros. Los posibles beneficios de la diversificación se puede aumentar considerablemente, si añadimos otras clases de acciones en el análisis, lo que tendría correlación baja o negativa con los demás. Es difícil de imaginar que tipo de oportunidades se obtendrán en ese caso para la aplicación del método PQM de análisis de mercado y comercio.
Consulte el principio del artículo "Estructura del Portfolio de optimización a través del Método PQM (parte 1)"
Artículos previos
- El cuarto postulado de la Teoría de Dow: sirviendo al inversor
- Spread de portafolio a base de futuros continuos
- Portfolio de Sharpe – "Tres Líderes"
- El Método de Cotización del Portafolio para el Análisis de Portafolios "buenos" y "malos"
- Optimización del Portafolio a través del Método PQM (Parte 1)
- Construcción y Análisis de Portafolios de Acciones con el Método de Cotización del Portafolio PQM
